Эконометрические
программы
Эконометрические
|
|
Econometric
|
|
Оценивание пороговой авторегрессии. Версия: 09.2005 |
Estimating threshold autoregression. Version: 09.2005 |
Пороговая авторегрессия (ПАР) определяется как
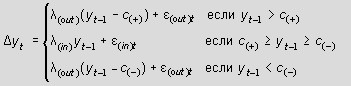 где y - временной ряд (t = 1,...,T). Более подробное описание модели и её приложение см. в LICOS DP No. 152/2004. Программа оценки параметров ПАР (авторегрессионных коэффициентов λ и порогов с) и тестирования на пороговый эффект реализована в виде макроса Microsoft Excel. Упакованный файл содержит инструкцию к программе (в формате pdf) и файл Excel с контрольным примером и макросом программы. |
The threshold autoregression (TAR) is specified as
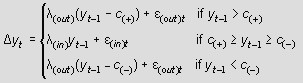 where y is a time series (t = 1,...,T). See LICOS DP No. 152/2004 for more details and an application. The program for estimating TAR parameters (namely, autoregressive coefficients λ and thresholds с) and testing for the threshold effect is organized as a Microsoft Excel macro. A compressed file contains instructions (in pdf format) and an Excel file with a test example and the program macro. |
| Скачать (zip, 355 k) | Download (zip, 280 k) |
|
Нелинейный тест на единичный корень при структурном скачке среднего. Версия: 08.2005 |
Nonlinear unit root test in the presence of a structural break in the mean. Version: 08.2005 |
Пусть временной ряд y имеет структурный скачок в t = θ + 1.
Обычно для тестирования такого ряда
на единичный корень используется линейная модель Перрона -
b.jpg) (t = 1,...,T),
где .jpg) = 0, если t ≤ θ,
и = 1, если t > θ. Однако
для более точного описания процесса на коэффициенты должно быть наложено нелинейное
ограничение ψ = -λδ/(λ + 1). Такой нелинейный тест
оказывается более мощным, чем тест Перрона, причём асимптотическими распределениями
статистики нелинейного теста являются распределения Дикки-Фуллера.Подробности - в MPRA Paper No. 678. Программы тестирования на единичный корень, получения p-значений теста и дополнительные программы реализованы в виде программ для EViews. Материалы содержатся в двух упакованных файлах: первый включает инструкцию к программам (в формате pdf, по-английски) и сами программы, второй -- файл Excel с p-значениями тестовых статистик. |
Let a time series y has a structural break at t = θ + 1.
Commonly, to test such a series for a unit root, the Perron's linear model is used,
(t = 1,...,T),
where = 0 if t ≤ θ
and = 1 if t > θ.
However, to more adequately describe the underlying process, nonlinear constraint
ψ = -λδ/(λ + 1) should be imposed on the coefficients. Such a nonlinear
test is more powerful than the Perron test, the asymptotic distributions
of the nonlinear test statistics coinciding with the Dickey-Fuller distributions. For details, see MPRA Paper No. 678. The program for unit root testing and the program for deriving p-values of the test as well as additional ones are organized as EViews programs. Two compessed files contain the material: the first one comprises instructions (in pdf format) and the programs themselves, and the second one comprises an Excel file with p-values of the test statistics. |
|
Скачать: программы и инструкцию (zip, 410 k) файл p-значений (zip, 2.7 Mb) |
Download: programs and instructions (zip, 410 k) file of p-values (zip, 2.7 Mb) |
|
Оценка и тестирование на единичный корень моделей временных рядов с асимптотически затухающим трендом. Версия: 07.2021 |
Estimating and testing for unit root time series models with asymptotically decaying trend. Version: 07.2021 |
Авторегрессионный процесс АР(1) с нелинейным асимптотически затухающим трендом
может моделировать конвергенцию доходов, душевого ВВП, выпусков, цен/уровней
цен и т.д. в исследованиях экономического роста или паритета покупательной
способности/закона единой цены. Более подробное описание и приложение см., например, в MPRA Paper No. 99316. Конкретными видами трендов являются логарифмически-экспоненциальный, экспоненциальный и дробный. Программы оценки таких моделей и тестирования их на единичный корень, а также программы получения p-значений теста на единичный корень реализованы в виде программ для EViews. Упакованный файл ниже содержит инструкцию к программам (в формате pdf, по-английски), сами программы и файл Excel с p-значениями тестовых статистик. |
An AR(1) autoregressive process with nonlinear asymptotically decaying trend
can model convergence of incomes, GDP per capita, output, prices/price levels,
etc. in the context of economic growth or purchasing power
parity/the law of one price. See, e.g., MPRA Paper No. 99316 for details and an application. Specific forms of the trend are the log-exponential trend, exponential trend, and fractional trend. The programs for estimating such models and testing them for unit root as well as the programs for deriving p-values of the unit root test are organized as EViews programs. The compressed file below contains instructions (in pdf format), the programs themselves, and an Excel file with p-values of the test statistics. |
| Скачать (zip, 756 k) | Download (zip, 756 k) |